Линейные операции над векторами

Линейные операции называются операции сложения и вычитания векторов и умножение вектора на число.

§ Сумма векторов Определение 1. Пусть и — два свободных вектора. Возьмём произвольную точку О и построим вектор =, в затем от точки, А отложим вектор =. Вектор, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается +.

Это правило построения суммы двух векторов называется «правилом треугольника».

Определение 2. Суммой векторов и с координатами а_1, а₂ и в_1, в₂ называется вектор с координатами а₁+в_1, а₂+в_2, т. е.

(а₁; а₂)+ (в₁; в₂) = (а₁+в₁; а₂+в₂).

Ту же самую сумму векторов можно получить иным способом.

Отложим от точки О вектор = и =. Построим на этих векторах как на сторонах параллелограмм ОАВС. Вектор, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов +. Из рисунка непосредственно следует, что сумма двух векторов обладает переместительным свойством:

+=+.

Сумма двух векторов, исходящих из одной точки, выполняется по «правилу параллелограмма».

Пусть, например, даны три вектора, и .

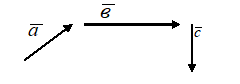
Построим сначала сумму векторов +, а затем, прибавив к этой сумме, получим вектор (+)+. На рисунке =, =, =+, = и =+=(+)+.

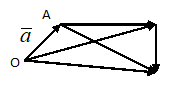
Из рисунка видно, что тот же вектор мы получим, если к вектору = прибавим вектор =+.Таким образом, (+)+=+(+), т. е. сумма векторов обладает сочетательным свойством. Поэтому сумму трёх векторов, и записывают просто ++.

Аналогично можно построить сумму четырёх, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется «правилом многоугольника».

=++++.

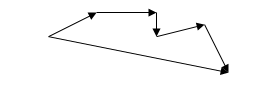
Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго; к концу второго — начало третьего и т. д. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов.

Если при сложении нескольких векторов конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нулевому вектору. Очевидно, что для любого вектора имеет место равенство +0=.

§ Разность векторов Разностью векторов и называется такой вектор =-, сумма которого с вычитаемым вектором дает вектор. Таким образом, если =-, то + =.

Разность векторов и обозначается так: — .

Из определения суммы двух векторов вытекает правило построения вектора — разности. Откладываем векторы = и = из общей точки О. Вектор, соединяющий концы уменьшаемого вектора и вычитаемого вектора, является разностью =-. Действительно, по правилу сложения векторов +=, или + =.

Задачу о построении разности двух векторов можно решить и другим способом.

Пусть даны векторы и справедливо равенство -=+(-).

Вектор — называется противоположным вектору, если вектор и — имеют равные длины и противоположно направлены.

Вектором, противоположным нулевому вектору, считается нулевой вектор.

Если — противоположный вектору, то, очевидно, +(-)= 0.

§ Произведение вектора на число.

Произведением ненулевого вектора и на число k называется такой вектор, длина которого равна, причем векторы и соноправлены при k>=0 и противоположно направлены при k<0. Произведением ненулевого вектора на любое число считается ненулевой вектор.

Произведение вектора на число k обозначается так: k*.

На рисунке изображены вектор и векторы 3*, -1,5*.

Из определения произведения вектора на число непосредственно следует, что:

• 1) произведение любого вектора на число нуль есть нулевой вектор;
• 2) для любого числа k и любого вектора векторы и k* коллинеарны

Умножение вектора на число обладает следующими основными свойствами (для любых чисел k, l и любых векторов ,) :

• 1. (k*l)* =k*(l*)-сочетательный закон
• 2. (k+l)* =k*+l*
• 3. k*(+)=k*+k*