Основные уравнения моментной теории тонких оболочек

Вырежем из оболочки постоянной толщины h нормальными сечениями криволинейный четырехугольный элемент (рис. 7.16), стороны которого ограничены координатными линиями и, v и и + du, v + dv, располагающимися на срединной поверхности оболочки. Срединная поверхность находится на равном расстоянии от внешней и внутренней поверхностей оболочки. На стороны вырезанного фрагмента оболочки действуют внутренние усилия и моменты: 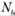, 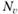- нормальные усилия, 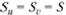- касательные усилия, 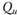,  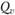— поперечные силы; 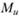,  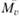— изгибающие моменты,  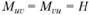— крутящие моменты. Размерность усилий — Н/м, т. е. ньютон на метр длины соответствующей координатной линии; размерность изгибающих и крутящих моментов — Н • м/м, т. е. Н • м на метр длины соответствующей координатной линии.

Принимая во внимание размерность усилий и моментов, для составления уравнений равновесия значения усилий и моментов, показанные на рис. 7.16, необходимо умножить на соответствующие длины сторон, где приложены эти усилия и моменты.

Будем считать, что криволинейная координатная сеть и, v ортогональная (F= 0) и сопряженная (М = 0), т. е. координатные линии представляют собой линии главных кривизн.

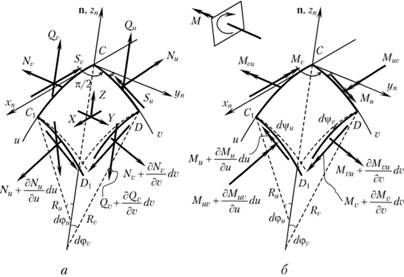
Рис. 7.1 в. Криволинейный четырехугольный элемент CCiDlD, вырезанный из срединной поверхности оболочки.

Обозначим через X, Y, Z интенсивность внешней распределенной поверхностной нагрузки (Н/м2 поверхности).

Составим уравнения равновесия относительно подвижных ортогональных осей координат (см. рис. 7.16): 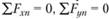, 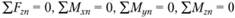и получим соответственно.

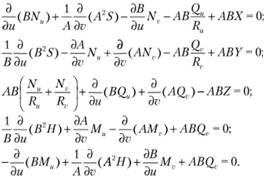(7.1).

Последнее шестое уравнение равновесия 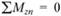считается тождеством, так как принято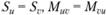

Обозначим перемещения произвольной точки срединной поверхности оболочки в направлении касательных к координатным линиям и, v и в направлении нормали к поверхности через 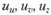соответственно.

Обозначим через 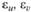относительные деформации в направлении координатных линий и, v, а через 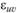- сдвиг, т. е. изменение угла между координатными линиями.

Введем дополнительно три параметра, характеризующие изгибную деформацию срединной поверхности оболочки:

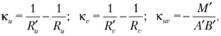
где 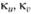- параметры изменения кривизн координатных линий и, v соответственно; 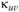- кручение элемента оболочки.

Параметры со штрихами — это параметры для деформированной оболочки.

Геометрические уравнения теории оболочек связывают между собой перемещения и деформации срединной поверхности оболочки. При выводе геометрических уравнений считают, что нормальный к срединной поверхности прямолинейный элемент оболочки остается прямолинейным и перпендикулярным к деформированной поверхности и после деформации. Для системы координат в линиях кривизн они будут иметь вид.

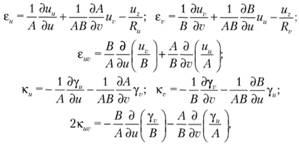(7.2).

где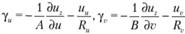

В последних двух выражениях имеем, что 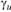- угол, на который поворачивается вектор 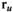в сторону вектора? в плоскости (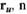);  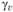— угол, на который поворачивается вектор 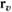в сторону вектора n в плоскости ().

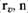Физические уравнения (закон Гука в теории оболочек) имеют вид.

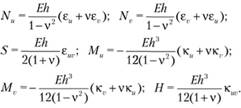(7.3).

Таким образом, при расчете оболочек толщиной h, заданных в линиях кривизны, вводятся следующие двумерные, зависящие от двух переменных и, v, величины:

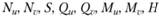- внутренние силовые факторы;

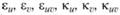- компоненты тангенциальной и изгибной деформаций;

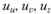- компоненты смещения.

Всего вводится 17 величин, для которых получены следующие расчетные уравнения моментной теории оболочек:

• • пять уравнений равновесия (7.1) бесконечно малого элемента оболочки, которые связывают между собой внутренние силовые факторы;
• • шесть соотношений (7.2) между деформациями и перемещениями;
• • шесть формул (7.3), связывающих между собой внутренние силовые факторы и деформации срединной поверхности оболочки.

Итого имеем 17 расчетных уравнений для определения 17 двумерных параметров.