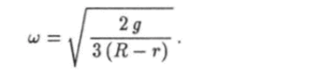Принцип наименьшего действия. 
Уравнения Лагранжа

Движение системы, имеющей s степеней свободы, можно описать посредством функций q 1 = 9i (i),…, q$ = qs (t)t определяющих зависимость обобщенных координат от времени t. Для краткости всю совокупность этих функций обозначим так:

Производные q_a от обобщенных координат q_Q = q₀(t) по времени t называются обобщенными скоростями:

Используя функции (14.21), кинетическую.

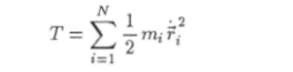
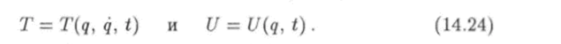
Функцией Лагранжа (Жозеф Лагранж (1736 — 1813) — французский математик) называется функция и потенциальную V = U (r,…, гуу, f) энергии системы можно выразить через обобщенные координаты и скорости и время I, т. е. представить их в виде.

Уравнениями движения механической системы называются дифференциальные уравнения, решениями которых являются функции (14.23), описывающие движение этой системы. Для системы с идеальными связями, в которой действуют только потенциальные активные силы, уравнения движения могут быть получены из принципа наименьшего действия или принципа Гамильтона (Уильям Гамильтон (1805 — 1865) — ирландский математик и физик).

Пусть q = q (t) есть произвольная непрерывно дифференцируемая функция, удовлетворяющая условиям.

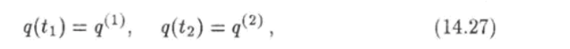
где qW и qW — значения обобщенных координат, характеризующие какието два положения 1 и 2 системы в пространстве. Функционал 5 от функции

называется действием Согласно принципу Гамильтона среди всех возможных функций q = q (l), удовлетворяющих условиям (14.27), только та описывает действительное движение механической системы из положения 1 в положение 2, для которой действие (14.28) принимает наименьшее значение. В силу теорем, доказанных в разделе 14.1, из принципа Гамильтона вытекает, что действительное движение системы описывается функцией q = q (t)_} которая является экстремалью функционала (14.28), т. е. для этой функции выполняется необходимое условие экстремума функционала (14.28):

для действительной траектории q = g (<) движения системы. Из условия (14.29) в свою очередь следует, что экстремаль q = q (t) должна удовлетворять уравнению Эйлера:

от обобщенных координат и скоростей механической системы и времени t_} равная разности кинетической и потенциальной энергий:

С учетом того, что q есть многомерная величина (14.23), символическое уравнение (14.30) нужно рассматривать как систему из $ уравнений для функций q_Q = q_a(t) :

где 0=1,2, s. В аналитической механике уравнения (14.31) называются уравнениями Лагранжа.

Приведем несколько примеров, демонстрирующих получение уравнений Лагранжа для некоторых механических систем.

Пример 1. Тело массы т движется вдоль оси х в потенциальном поле U = U (x, t). Это движение удобно описать посредством зависимости координаты тела от времени, т. е. функции х = x (t). В этом случае функция Лагранжа (14.26) будет иметь вид.

Как видно, здесь роль обобщенной координаты играет декартова координата х. Зная функцию Лагранжа, составим уравнение движения.

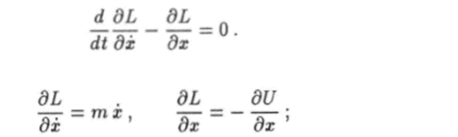
Так как.

придем к уравнению которое можно записать в виде.

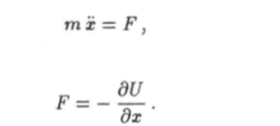
где Таким образом, уравнение Лагранжа для прямолинейного движения эквивалентно второму закону Ньютона.

Пример 2. Пусть в пространстве имеется N материальных точек. Положение каждой из этих точек можно задать при помощи радиусвектора rj (t = 1, 2,…, N). Так как радиус-вектор г, имеет три координаты Xj, у,, Zi, такая система будет иметь 3N степеней свободы. Возьмем где т, — масса г-й частицы, U — потенциальная энергия системы. Теперь можно составить уравнение Лагранжа Так как.

уравнение Лагранжа (14.33) принимает вид где.

где.

— сила, действующая на i-ю частицу. Таким образом, из принципа Гамильтона вытекают ньютоновские уравнения движения.

Пример 3. Однородный цилиндр массы т и радиуса г катится без скольжения по внутренней поверхности неподвижного цилиндра радиуса R > г (рис. 14.7). Такая система имеет только одну степень свободы. Будем описывать ее движение при помощи функции у? =.

Составим функцию Лагранжа. Для этого сначала найдем кинетическую энергию тела. Так как цилиндр катится без скольжения, прямая А соприкосновения цилиндрических поверхностей является мгновенной осью вращения цилиндра. Поэтому его кинетическую энергию можно найти по формуле (6.27).

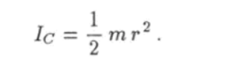
в качестве обобщенных координат этой системы декартовы координаты материальных точек и запишем функцию Лагранжа:

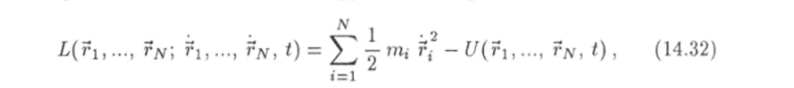
где 1_А — момент инерции цилиндра относительно мгновенной оси вращения, — его угловая скорость. Момент инерции однородного цилиндра относительно оси, проходящей через его центр масс, согласно формуле (6.30) равен.

Рис. Ц.1. Для этой системы угол ф есть обобщенная координата.

С учетом того, что расстояние от центра масс до мгновенной оси вращения равно г, угловую скорость цилиндра найдем по формуле Эйлера.

(2.47):

где v_c — скорость центра масс катящегося цилиндра. Координаты центра масс связаны с углом <�р соотношениями.

Продифференцировав эти функции по времени /, получим следующие выражения для координат вектора скорости центра масс.

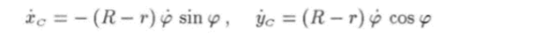
и его модуля Используя формулы (14.35) — (14.38), найдем зависимость кинетической энергии от обобщенной скорости ф :

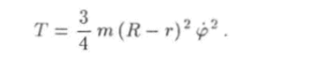
Потенциальная энергия цилиндра в однородном поле силы тяжести равна.

При этом функция Лагранжа будет иметь вид 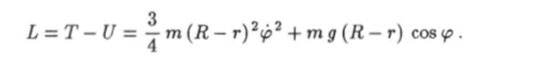Подстановка этой функции в уравнение Лагранжа.

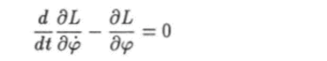
после несложных преобразований приводит к уравнению движения цилиндра.

Когда цилиндр движется так, что угол у? все время остается малым, можно положить sin ~ у?. При этом условии уравнение (14.39) будет описывать гармонические колебания с частотой.