Классическая теория ионизационного торможения

Классическая теория торможения тяжелых заряженных частиц основывается на представлении о том, что проходящая через вещество частица взаимодействует с атомными электронами как с независимыми свободными частицами. При этом потери энерг ии частицей за счет ее взаимодействия с отдельными электронами просто суммируются в предположении равномерного распределения электронов в веществе. Допускается также, что потери энергии частицы при столкновении с одним электроном настолько малы, что искривление ее траектории ничтожно: частица движется прямолинейно (о чем свидетельствуют треки в камере Вильсона и т. д.) и равномерно. Кроме того, частица пролетает мимо электрона настолько быстро, что последний не успевает изменить своего положения в пространстве за время столкновения.

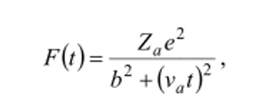
Рассмотрим взаимодействие быстрой (но нерелятивистской) тяжелой заряженной частицы, несущей заряд с одним из электронов вещества. Пусть частица пролетает мимо него с постоянной скоростью v_a по прямолинейной траектории с прицельным параметром b (рис. 19.2). Разложим кулоновскую силу действующую в каждый момент времени / со стороны частицы на электрон, на продольную и поперечную составляющие /^гц (/) и F±(t). Согласно сформулированным выше допущениям продольный импульс силы }F (t)dt, полученный за время / 0. Поперечный же импульс силы оказывается равным.

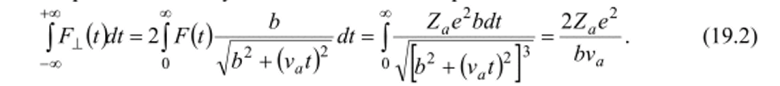
Приравняв его к импульсу (количеству движения) электрона р_е, вычислим кинетическую энергию электрона после его взаимодействия с пролетевшей частицей:

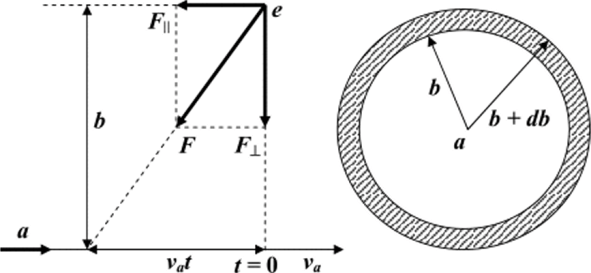
Рис. 19.2. К выводу формулы для ионизационных потерь энергии тяжелыми частицами.

Такова потеря энергии частицы при взаимодействии с одним электроном, отстоящим от траектории се движения на расстоянии Ь. Далее, пусть частица проходит слой вещества dx. Вырежем в нем мысленно тонкий кольцевой цилиндр, гак чтобы его ось совпадала с траекторией движения частицы. Число электронов в этом кольцевом пилинлпе оавно.

где - плотность атомных электронов в веществе. Потери энергии частицы за счет взаимодействия с этими электронами составляют T_edN_e. Чтобы получить всю величину потерь энергии частицы при прохождении слоя dx, необходимо проинтегрировать (19.3) но плоскости, в которой лежит этот слой вещества:

Отсюда для тормозной способности вещества получаем.

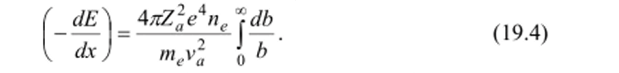
Стоящий в правой части выражения (19.4) интеграл логарифмически расходится. Однако физическая интуиция подсказывает, что вычисление его в пределах от 0 до со неразумно, так как при слишком малых и при слишком больших h мы выходим за границы предположений, которые сформулировали выше. Действительно, при Ь->0 бессмысленно считать, что электрон после взаимодействия с частицей сохранил свое положение в пространстве: ведь он получает при таком столкновении большую энергию: порядка 2m_ev_a². С другой стороны, при Ь—*со энергия, получаемая электроном, оказывается меньше потенциала ионизации и даже меньше порога возбуждения атома. В этом случае предположение о независимых свободных электронах вступает в противоречие с реальной картиной строения вещества. Учет этих соображений даст следующий результат:

4*Zje⁴n_e

^me^vl

где Ь_тп и Ь_тах — минимальное и максимальное значения прицельного параметра, в пределах которых должно проводиться интегрирование. Для получения простейшей оценки тормозной способности отношение прицельных параметров в (19.5) можно заменить отношением максимальной и минимальной энергии, полученной электроном. Тогда.

где I — средний потенциал ионизации вещества, обычно определяемый из эмпирически установленного соотношения /= 13,5−2' эВ.