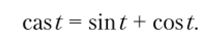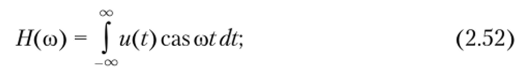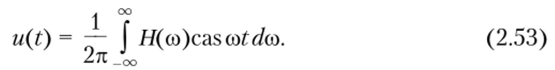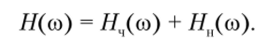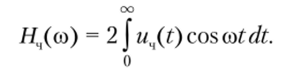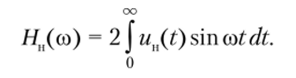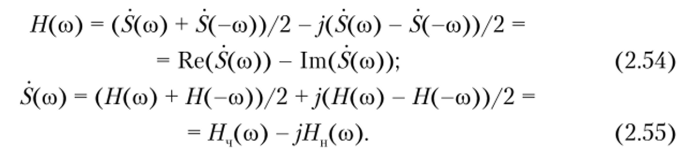Преобразования Хартли в спектральном анализе сигналов
Один из недостатков представления сигналов с помощью преобразования Фурье — использование в нем комплексных чисел. Обработку же ряда сигналов в виде последовательности вещественных данных желательно осуществлять в области действительных чисел. Этим свойством обладает преобразование Хартли. Преобразование Хартли определяют как разность вещественной и мнимой составляющих преобразования Фурье… Читать ещё >
Преобразования Хартли в спектральном анализе сигналов (реферат, курсовая, диплом, контрольная)
Один из недостатков представления сигналов с помощью преобразования Фурье — использование в нем комплексных чисел. Обработку же ряда сигналов в виде последовательности вещественных данных желательно осуществлять в области действительных чисел. Этим свойством обладает преобразование Хартли.
Р. Хартли еще в 1942 г. предложил пару интегральных преобразований сигналов — прямое и обратное, основанные на специально введенной им функции.
Для сигнала u (t) прямое и обратное преобразования Хартли имеют вид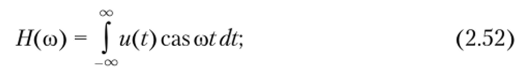 
Представляя сигнал как сумму четной и нечетной составляющих, запишем прямое преобразование Хартли в виде.
Если исследуемый сигнал — четная функция u4(t)9 то из соотношения (2.52) находим.
Для сигнала в виде нечетной функции un(t) из соотношения (2.52) имеем следующую форму преобразования Хартли:
Сравнение преобразований Хартли //(со) и Фурье 5(со) позволяет установить взаимосвязь между ними. После сопоставлений формул (2.29) и (2.52) получим.
Преобразование Хартли определяют как разность вещественной и мнимой составляющих преобразования Фурье; преобразование Фурье равно разности четной и нечетной составляющих преобразований Хартли, умноженных на ].
Из формулы (2.55) следует, что для сигнала, описываемого четной функцией, Я (со) = 5(со), а для сигнала, описываемого нечетной функцией, //(со) = -jS ( со).