Задачи по композиции

Рассмотрим задачи на использование приведенных формул (задачи 4.52—4.55 — на формулу (4.8), 4.56—4.58 — на формулу (4.9), 4.59 — на формулу (4.10)).

Задача 4.52. СВ X и Yнезависимы, X ~ Е (Х_{), У ~ Е (₂), т. е.

/(х) и /₂(х) — соответственно плотности распределения СВ X и Y. Найти плотность распределения g (z) СВ Z = X + У.

Решение

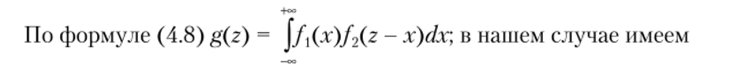
Задача 4.53. СВ Хи Yнезависимы, СВ X ~ N (a_u а,), СВ У ~ Х (а₂, ст₂). Найти fztz) — плотность распределения СВ Z = X + У.

Решение

По формуле (4.8).

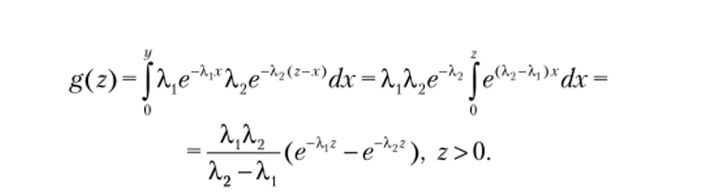
При А, = Х₂ это обобщенный закон Эрланга второго порядка с плотностью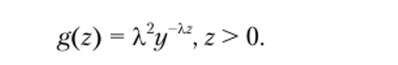

Задача 4.54. Найти плотность суммы двух независимых СВ X и У, имеющих^{-распределение} с параметрами k и / (степенями свободы) соответственно: X ~ xjj; У ~ Х/;

Решение

Определим индикаторную функцию J (z) ⁼ | | ^ > o'.

Тогда плотности распределения СВ X и yg,(.r) ng₂(jy) есть соответственно.

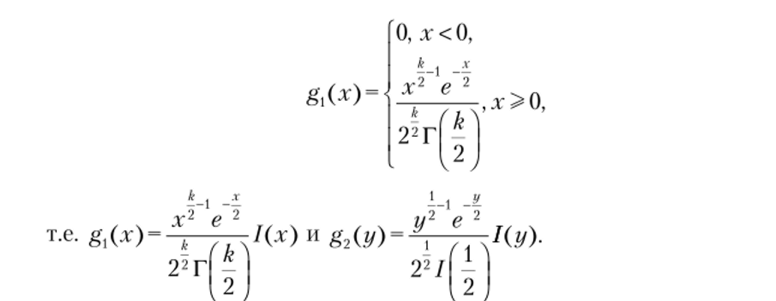
В дальнейшем будет использована бета-функция В (/?, q) 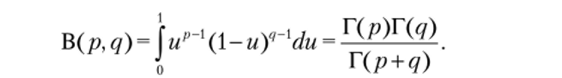Для Z = X + Y по формуле (4.8).

Замечание 45. По индукции легко установить, что сумма независимых СВ, распределенных по %², имеет^{-распределение} с числом степеней свободы, равным сумме чисел степеней свободы слагаемых СВ.

Задача 4.55. СВ X и Y — независимы и имеют гамма-распределение: X ~ Г_{а х}, Y- Г_рд. Найти плотность распределения g (z) CBZ = X + Y. Решение

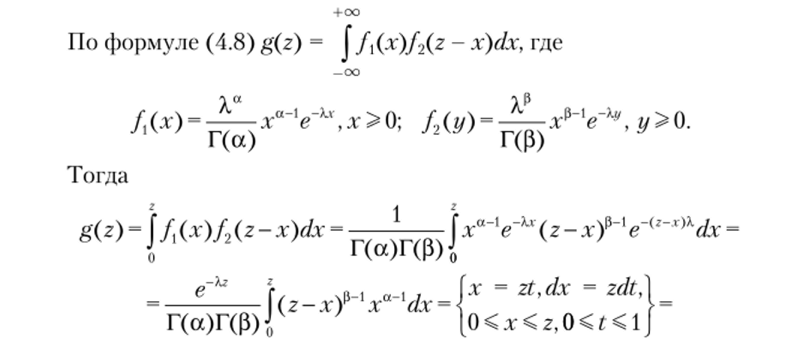
Замечание 4.6. По индукции очевидно, что если СВ Х_и …, Х_п независимы и имеют соответственно гамма-распределения Г_{а) х}, Г_{а х},.

п

…, Г_{а }}, то Z = имеет гамма-распределение Г*.

/=о.

1−1.

Задача 4.56. Пусть X и У — соответственно моменты первого и второго успехов в серии испытаний Бернулли Найти распределение СВ У при фиксированном значении СВ X.

Решение

Введем CBZ = У — X => У = X + Z, где СВ X и Z независимы и одинаково распределены. Тогда.

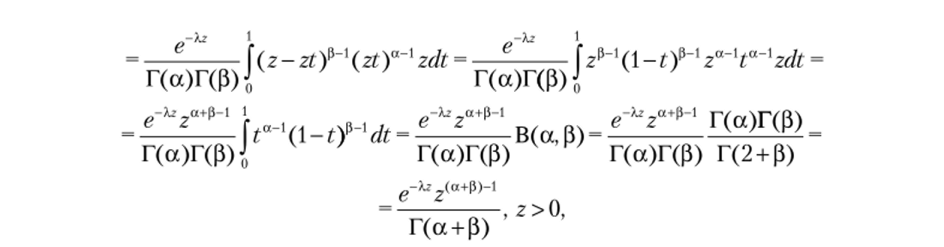
а это плотность гамма-распределения Г_а+р_Д.

Замечание 4.7. Этот результат сразу следует из смысла распределения Паскаля.

Задача 4.57. СВ X, У независимы, X ~ П (^), У — ЩХ₂)_} Z = X + У. Найти P (Z = п).

Решение

Замечание 4.8. По индукции легко установить, что если Х_и…, Х_т — независимые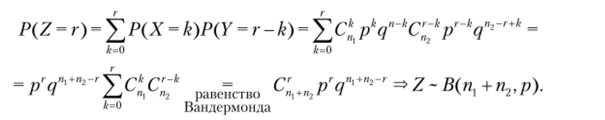

Задача4.58. СВХ~В (п_ир)₉ Y~ В (п₂,р), Xи У—независимые. Найти распределение СВ Z = X + У.

П п₂

1- й способ. Представим СВ X и Укак суммы: X = Х^С Y = X У, где.

<-1 7=1.

п,+м₂

{Хф {К,} — независимые СВ ~ В (1,р). Тогда СВ Z = X + Y = X V*, где.

к-1

{V*} — независимые СВ, имеющие распределение В ( 1, р), => СВ Z — ~В (щ + п₂, р).

П

2- й способ. Используем равенство Вандермонда С" = ^C^k_MC" _s

к=0

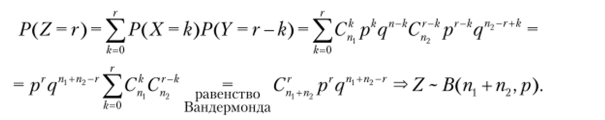
Замечание 4.9. По индукции легко установить, что если X, …,.

П

Х" — независимые СВ, где X; ~ B (n_it р), i = 1,…, n, Z= XX,-, то СВ.

/. л.

Z-В ^п_гр .

Задача 4.59. СВ X и У независимы; X задана рядом распределения.

У — Х (0,1); Z= 2Х+ У. Найти /(Х) — функцию распределения СВ Z. Решение

Строим ряд распределения СВ X, = 2Х:

I^х (t²

где Ф (.г) = —j= fexp—dt — табличная функция Лапласа.

42nl 2.