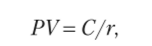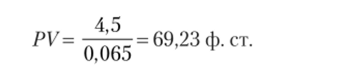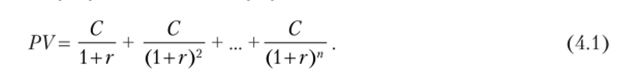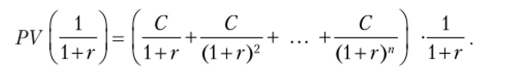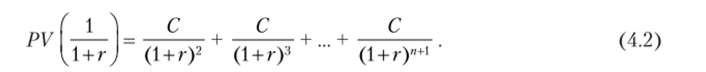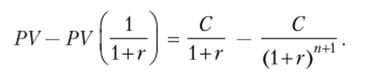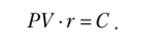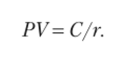Бессрочная рента и аннуитет

Бессрочная рента

Среди финансовых инструментов можно встретить такие, которые в течение неограниченного периода дают постоянный доход. Примером могут служить британские консоли (консолидированные облигации), выпущенные британским правительством еще во время войн с Наполеоном. У этих облигаций нет конечного срока обращения, и они до сих пор обращаются на британском фондовом рынке. По этим облигациям ежегодно их владельцы получают 4,5 фунта стерлингов в виде дохода. Данные ценные бумаги не имеют срока погашения и, следовательно, инвестор в течение бесконечного отрезка времени получает фиксированный годовой доход.

Фиксированные равновеликие платежи, совершаемые через одинаковые промежутки времени, в течение неограниченного срока называются бессрочной рентой.

Как определить текущую стоимость бессрочной ренты? Вернемся к нашему примеру с британскими консолями. Если известно ежегодное поступление по данной облигации, то текущая цена этой ценной бумаги определяется по формуле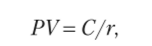

где PV — текущая (приведенная) стоимость; С — постоянный годовой доход; г — требуемая годовая доходность (ставка дисконтирования).

Если годовая доходность, которую требует инвестор по государственным ценным бумагам британского правительства, составляет 6,5%, а по облигациям ежегодно выплачивается 4,5 фунта стерлингов (ф. ст.), то текущая стоимость облигации составит: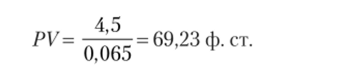

Формула определения текущей стоимости, как мы видим, достаточно проста. Однако насколько она корректна? Давайте проверим и выведем эту формулу из классической формулы приведенной стоимости.

1. Определим текущую стоимость будущих платежей:

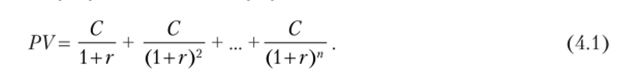
2. Умножим обе части уравнения на :

3. В результате получим.

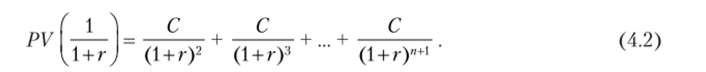
4. Вычтем из уравнения (4.1) уравнение (4.2):

Если операция совершается на бессрочном периоде действия, т. е. п стремится к бесконечности, то выражение становится бесконечно малой величиной, которой можно пренебречь. В этом случае мы получаем.

5. Умножим обе части на (1 + г):

6. Отсюда приведенная стоимость.