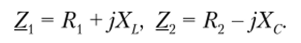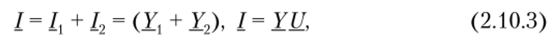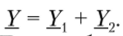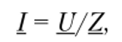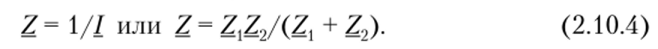Параллельное соединение элементов в цепи синусоидального тока
Двух ветвей Пусть напряжение на входных полюсах, А и В цепи равно Ц. Тогда каждая из ветвей представляет собой последовательное соединение элементов с заданными сопротивлениями и одним напряжением. Токи в ветвях, согласно закону Ома, равны. Соотношение между комплексным током и напряжением можно представить через эквивалентное комплексное сопротивление 2, как и для цепи с последовательным… Читать ещё >
Параллельное соединение элементов в цепи синусоидального тока (реферат, курсовая, диплом, контрольная)
Эквивалентные проводимость и сопротивление. Электрическая цепь с параллельным соединением элементов в общем случае состоит из ряда ветвей, включенных между двумя узлами. Рассмотрим, например, электрическую цепь, состоящую из двух ветвей, схема замещения которой изображена на рис. 2.10.1.
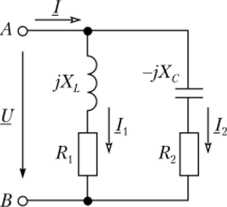
Рис. 2.10.1. Схема замещения электрической цепи с параллельным соединением.
двух ветвей Пусть напряжение на входных полюсах А и В цепи равно Ц. Тогда каждая из ветвей представляет собой последовательное соединение элементов с заданными сопротивлениями и одним напряжением. Токи в ветвях, согласно закону Ома, равны.
где ZxwZ2 — эквивалентные комплексные сопротивления ветвей,.
Уравнения (2.10.1) можно записать иначе, если ввести эквивалентные комплексные проводимости ветвей:
Входной ток цепи, согласно первому закону Кирхгофа, в комплексной форме равен сумме токов ветвей:
где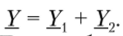 
Таким образом, входные ток I и напряжение Ц цепи с параллельным соединением ветвей можно связать через эквивалентную комплексную проводимость цепи У, которая равна сумме комплексных проводимостей ветвей. Этот вывод можно распространить на цепь с любым количеством параллельно соединенных ветвей.
Соотношение между комплексным током и напряжением можно представить через эквивалентное комплексное сопротивление 2, как и для цепи с последовательным соединением элементов, но закону Ома:
где 7— эквивалентное комплексное сопротивление цепи,.
Формула (2.10.4) для комплексного эквивалентного сопротивления двух параллельных ветвей аналогична по форме соответствующей формуле для цепей постоянного тока.