Необходимые сведения из линейной алгебры

Вначале мы кратко рассмотрим некоторые основные определения из линейной алгебры, которые необходимы для понимания матричных вычислений. В дальнейшем мы будем предполагать, что матрицы и вектора вещественные. Тогда вектора представляют собой элементы JV-мерного евклидова пространства К^Л. В этом пространстве определены следующие операции:

• сложение

• умножение на скаляр

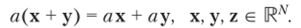
В дополнение любой паре векторов х, у е R* ставится в соответствие вещественное число (х, у), которое называется скалярным произведением. Для скалярного произведения постулируются следующие аксиомы:

Векторы-столбцы.

образуют стандартный базис в (R ^v Все другие вектора могут быть разложены по базису Ь" (и = 1,…, N):

Коэффициенты х" представляют собой компоненты вектора х, и это представление обычно записывается в компактной форме: х = (х₍, x_v)¹. Надстрочный индекс Т обозначает операцию транспонирования, которая превращает векторы-столбцы в векторы-строки и наоборот. Скалярное произведение двух векторов х = (xj,x_N)¹ и у = (у_и …, y_N)¹ вычисляется следующим образом:

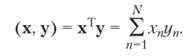
Два вектора хну ортогональны, если (х, у) = 0. Для того чтобы работать с каким-нибудь объектом, нам необходим способ его измерения. С этой целью вводится понятие нормы. Норма вектора х есть вещественное число ||х|| со следующими свойствами:

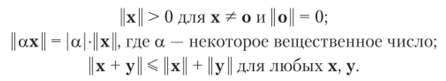
Для вектора х = (х_1;…, Хдг)^т вещественное число.

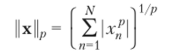
есть норма при любом значении р > 1 (р-норма Гёльдера). На практике часто применяются следующие нормы:

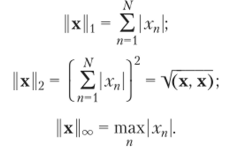
Каждая квадратная матрица образует линейный оператор в векторном пространстве R'^v. Если вектор у представляет собой линейную функцию вектора х, тогда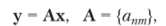

или.

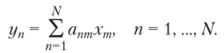
Правила операций над матрицами следуют из свойств линейных отображений. Так, С = А + В представляет собой сумму двух линейных функций заданных матрицами, А и В, где с_пт = а_пт + Ь_пт. Произведение АВ представляет собой результат применения отображения В, а затем отображения А. Если имеется у = А (Вх) = АВх = Сх, тогда компоненты матрицы С определяются по формуле.

Транспонирование матрицы, А осуществляется вращением, А относительно ее главной диагонали: А¹ = {а_птУ = = {а_тп}. Диагональная матрица D имеет все нулевые компоненты, кроме компонент d_n на главной диагонали:

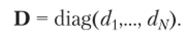
Теперь рассмотрим нормы матриц. Вещественное число || АI есть норма матрицы, если выполняются следующие условия:

|| А|| > 0 для, А О, где О обозначает нулевую матрицу и ЦО|| = 0;

|| а, А || = | а |*|| А ||, где, а — некоторое вещественное число;

На практике часто применяются следующие нормы:

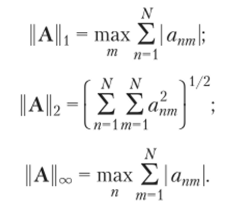
В дальнейшем символ || • || будет обозначать некоторую норму из рассмотренных выше норм. Матричная норма называется согласованной с векторной нормой, если ||Ах|| < ||А|| ||х||. Например, А_{ согласована с Цх^, ||А||₂ с ||х||₂ и ||А||оо с ||х||оо.

Свойство определенности матрицы играет важную роль в матричных вычислениях. Так, матрица, А называется положительно (отрицательно) определенной, если (х, Ах) > 0 (< 0) для всех ненулевых векторов х. Если знак скалярного произведения (х, Ах) зависит от вектора х, тогда матрица, А называется неопределенной.