Уравнения плоского движения жидкости в пласте

Для расчета плоского движения жидкости в пласте перечисленных характеристик одномерных фильтрационных потоков жидкости можно использовать два подхода. Первый из них вывод дифференциальных уравнений и их решение отдельно для прямолинейно-параллельного, плоскорадиального и радиально-сферического потоков жидкости и газа. Второй-вывод обобщенного уравнения одномерного течения флюида в недеформируемой трубке тока переменного сечения с использованием функции Лейбензона и получение из него конкретных формул применительно к различным схемам фильтрационных потоков. Второй подход более эффективен, позволяет исходить из обобщенных характеристик течения. Он используется в настоящем учебнике. В случае одномерного течения флюида в недеформируемой трубке тока переменного сечения (смотри рисунок 1.5) массовый расход по всей длине струйки сохраняется постоянным:

Qs=pQ=pwщ (s) =const, (2.1).

где s — координата, взятая вдоль линии тока, возрастающая по течению флюида.

Рисунок 1.5: Трубка тока.

Запишем закон Дарси (2.2) через функцию Лейбензона (2.3). Для этого умножим правую и левую части уравнения (2.2) на плотность флюида р (р) и на площадь сечения щ (s):

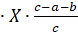
(2.2), (2.3).

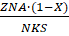
получим:

.

На основании формулы (2.3) можно заменить сdp = dР Тогда:

. (2.4).

Это дифференциальное уравнение является основным при расчете одномерных потоков.

Найдем из него распределение функции Лейбензона по длине струйки Р (s) и выведем формулу для расчета дебита. В уравнении (2.4) разделим переменные.

. (2.5).

и проинтегрируем в пределах от s=s₁ где известно значение функции Лейбензона Р=Р₁ до текущего значения s и соответствующего ему Р:

. (2.6).

Обозначим.

(2.7) Тогда.

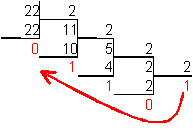
(2.8).

Интегрируя (2.5) по s в пределах от s₁ до s₂ и по P от P₁ до P₂, получим:

. (2.9).

Из последнего равенства найдем массовый расход:

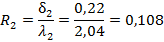
(2.10) где:. (2.11).

Формула (2.9) является аналогом закона Ома: силе тока соответствует дебит, электрическому потенциалу — функция Лейбензона, и по аналогии с электрическим сопротивлением знаменатель формулы (2.9) R_12, т. е. выражение (2.11), называют фильтрационным сопротивлением. Подставив выражение для массового расхода из (2.9) в (2.8), получим окончательно:

. (2.12).

Массовая скорость фильтрации определяется равенством:

. (2.13).

Из соотношения (2.12).

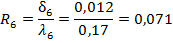
тогда:

. (2.14).

Зная конкретные зависимости плотности р и функции Лейбензона Р от давления для различных флюидов, а также выражения R_1s, R₁₂. щ (s) для разных одномерных потоков, можно рассчитать распределение давления p (s), скорости фильтрации w (s), получить формулы для массового и объемного расходов.

По распределению давления в дальнейшем найдем средневзвешенное по объему порового пространства пластовое давление, определяемое по формуле:

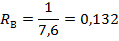
(2.15).

где Vn — общий объем порового пространства пласта.

Время движения отдельных частиц флюида определяется решением уравнения:

.

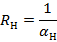
При условии, что в начальный момент t = 0 частица имела координату s = s₀, получим:

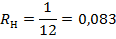
(2.16).

Запишем теперь полученные в общем виде формулы (2.10), (2.12), (2.14) в конкретном виде для каждого из одномерных потоков жидкости и газа.

Прямолинейно-параллельный фильтрационный поток

Площадь поперечного сечения щ = Bh = const; на контуре питания х₁ = 0, Р₁ = Р_к на галерее х₂ = L, Р₂ =Р_г, из R_1s = x/ (Bh), из (2.11) R₁₂ = L/ (Bh).

Тогда.

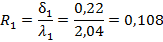
. (2.17).

(2.18).

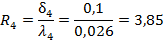
. (2.19).

Плоскорадиальный фильтрационный поток

Перейдем от координаты s к координате r, отсчитываемой от центра скважины. Для добывающей скважины s = R_к — r, так что ds = - dr; площадь фильтрационной поверхности щ (s) = 2рrh — боковая поверхность цилиндра; на контуре питания r₁ =R_k, P₁=P_k на забое скважины r₂ =r_c, P₂=P_k. Тогда.

.

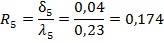
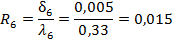
Из (2.10).

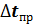
(2.20) Из (2.12).

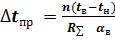
(2.21) Из (2.14).

. (2.22).

Радиально-сферический фильтрационный поток

В этом случае для добывающей скважины с полусферическим забоем имеем: s = Rx — r, ds = - dr, щ (s) = 2рr² — площадь поверхности полусферы с радиусом r; r₁= R_k, P₁ = P_k, r₂ = r_c, P₂ = P_с (смотри рисунок 1.4). Вычисляем фильтрационные сопротивления по формулам (2.7) и (2.11):

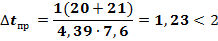
так как r_c << R_k.

Далее из (2.10), (2.12, (2.14) находим:

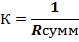
(2.23).

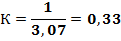
; (2.24).

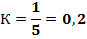
. (2.25).