Общая арифметическая средина или среднее весовое

Пусть имеем n результатов неравноточных измерений одной и той же величины 1_i и их веса Р_i

1₁, 1₂, 1₃,.. ., 1_n

Р₁, Р₂, Р₃,. .. , Р_n

Каждое значение 1_i можно рассматривать как среднее арифметическое из р_i равноточных измерений 1.

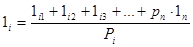
или Р_i 1_i = 1 _i.

Число таких равноточных измерений будет равно р. Взяв среднее арифметическое из левых и правых частей равенств, получим.

.

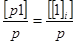
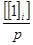
но = х_о — есть вероятнейшее значение (среднее арифметическое или арифметическая средина) согласно формуле (10).

Тогда.

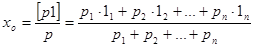
(63).

то есть общая арифметическая средина равна сумме произведений измерений и соответствующих весов, деленной на сумму весов измерений.

Средняя квадратическая погрешность общей арифметической средины На основании определения веса, используя формулу (56), можно написать.

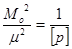
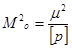
;, (64).

где M_o — средняя квадратическая погрешность общей арифметической средины, р — вес арифметической средины. Тогда.

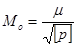
(65).

то есть средняя квадратическая погрешность общей арифметической средины равна средней квадратической погрешности отдельного измерения с весом, равным единице, деленной на корень квадратный из суммы весов данного ряда измерений.

Подставив сюда значение средней квадратической погрешности измерения с весом, равным единице (62), получим.

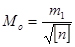
. (66).

то есть средняя квадратическая погрешность арифметической средины равна средней квадратической погрешности отдельного неравноточного измерения, деленной на корень квадратный из числа измерений.

Найти вероятнейшее значение угла (общую арифметическую средину) и его среднюю квадратическую погрешность.

Сначала определяем вес каждого результата, который можно принять равным числу приемов, гр. 3 (чем больше приемов, тем больше степень доверия к результату).

Затем находим общую арифметическую средину, которая будет равна сумме произведений результатов измерений (гр. 1) и соответствующих весов (гр. 3), деленной на сумму весов,.

.

После этого вычисляем вероятнейшие погрешности (гр. 4) по вышеприведенным зависимостям (д _i = 1_i — х_о) и все остальные величины (гр. 5−7).

Подставляя найденные величины в формулу (59) и дальше в формулу (65), получим.

.

; .

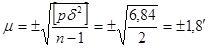
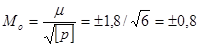
Пример. От трех марок высокоточного нивелирования определена техническим нивелированием отметка точки А.

Определить: а) вероятнейшее значение отметки точки А,.

• б) среднюю квадратическую погрешность результата с весом, равным единице,
• в) среднюю квадратическую погрешность отдельных результатов нивелирования,
• г) среднюю квадратическую погрешность вероятнейшего значения (общей арифметической средины).

Сначала определяем вес каждого результата нивелирования, который можно принять равным величине, обратной длине хода, гр. 3 (чем меньше длина хода, тем больше степень доверия к результату нивелирования). Умножив веса на 6, получим их величины в целых числах, гр. 4.

Затем находим общую арифметическую средину, по аналогии с предыдущим, то есть.

.

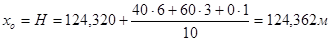
После этого вычисляем вероятнейшие погрешности и значения остальных граф табл. 6, гр. 5−7.

Подставляя найденные величины в формулы (59), (62) и (65), получим.

.

;; .

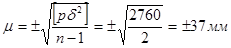
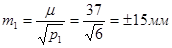
Следовательно, отметки точки, А были получены Н₁ = 124, 360 м15 мм, Н₂ = 124, 380 м21 мм, Н₃ = 124, 320 м37 мм.

Что касается общей арифметической средины, то.

и .

Из рассмотренных выше примеров видно, что в качестве весов можно принимать любые числа, характеризующие или отражающие степень доверия к результатам измерений, например, число приемов, длина хода.

Веса функций измеренных величин Для определения веса функций измеренных величин нужно воспользоваться формулами (33), (35), (37), (41) и (47), заменив в них средние квадратические погрешности величинами, обратными весу измерений. Тогда будем иметь.

1. Для функции вида Z = К. х.

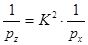
(67).

то есть число, обратное весу функции, равно произведению квадрата постоянной величины на число, обратное весу аргумента.

2. Для функции вида.

Z = х у.

(68).

то есть число, обратное весу функции, равно сумме чисел, обратных весам аргументов.

3. Для функции вида.

Z = х₁ х₂ х₃. .. х_n

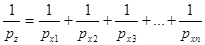
(69).

то есть число, обратное весу функции, равно сумме чисел, обратных весам аргументов.

4. Для функции вида.

Z = К₁х₁ К₂х₂ К₃х₃±. .. К_nх_n

(70).

то есть число, обратное весу функции, равно сумме произведений квадрата постоянного на число, обратное весу аргумента.

5. Для функции общего вида.

Z = f (x₁, x₂, х_3,. .. , x_n).

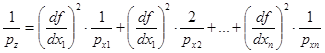
(71).

то есть число, обратное весу функции, равно сумме произведений квадрата частной производной по каждому аргументу на число, обратное весу соответствующего аргумента.