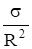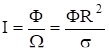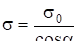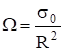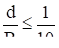Законы освещенности. 
Производственная санитария

Как показывают формулы (8.2) и (8.3), освещенность и сила света связаны между собой. Пусть точечный источник S освещает небольшую площадку у, расположенную на расстоянии R от источника (рис. 8.3).

Рис. 8.3. Освещенность, создаваемая точечным источником

Построим телесный угол Щ, вершина которого лежит в точке S и который опирается на края площадки у. Он равен. Поток, посылаемый источником в этот телесный угол, обозначим через Ф. Тогда.

.

.

отсюда.

(8.6).

т. е. освещенность площадки равна силе света, деленной на квадрат расстояния до точечного источника. Сравнивая освещенности площадок, расположенных на разных расстояниях R₁, R₂ от точечного источника, найдем; и т. д., или.

(8.7).

т. е. освещенность обратно пропорциональна квадрату расстояния от площадки до точечного источника. Это так называемый закон обратных квадратов.

Если бы площадка у была расположена не перпендикулярно к оси потока, а повернута на угол б, то она имела бы размеры.

.

где у₀ — площадка, пересекающая тот же телесный угол перпендикулярно к оси пучка, так что.

.

В таком случае освещенность площадки у.

(8.8).

Освещенность, создаваемая точечным источником на некоторой площадке, равна силе света, умноженной на косинус угла падения света на площадку и деленной на квадрат расстояния до источника.

Закон обратных квадратов соблюдается вполне строго для точечных источников. Если же размеры источника не очень малы по сравнению с расстоянием до освещаемой поверхности, то формула (8.6) не верна и освещенность убывает медленнее, чем по закону. Формула (8.6) дает вполне хорошее согласие с наблюдением при соотношении (d — размер источника).