Программирование алгоритма циклической структуры с известным числом повторений

Цель: овладение практическими навыками разработки, программирования вычислительного процесса циклической структуры с известным числом повторений.

Задания для самостоятельной подготовки:

• 1. Изучить теоретический материал об алгоритме циклической структуры и составление блок-схемы расчета.
• 2. Изучить операторов языка программирования и способы применения их в решении задачи на компьютере.
• 3. Построить блок-схему согласно заданию.
• 4. Составить программу решения задач.
• 5. Проверка программы по тестовому примеру.

Теоретическая часть:

Задание: составить структурную схему и написать программу с использованием оператора цикла FOR.

8 вариант:

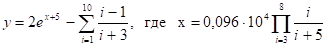
Блок-схема:

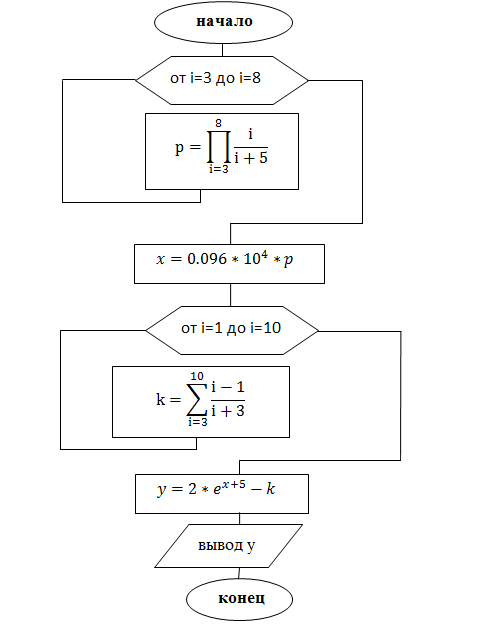
Программа:

#include.

#include.

using namespace std;

int main (){.

long long x=0,y, i, p=1,k=0;

for (i=3;i<=8;i++){.

p*=i/(i+5);

}.

x=0.096*pow (10,4)*p;

for (i=1;i<=10;i++){.

k+=(i-1)*pow ((i+3),-1);

}.

y=2*exp (x+5)-k;

cout<<" y="<

return 0;

}.

Результат: 296.

Решение систем линейных алгебраических уравнений

Цель: изучение численных методов решения систем линейных алгебраических уравнений, овладение навыками алгоритмизации, программирования и практического решения систем уравнений ПК.

Задания для самостоятельной подготовки Изучить:

метод Крамара;

метод Гаусса;

метод Гаусса с выбором главного элемента;

Разработать алгоритм решения в соответствии с заданием.

Составить программу решения задач.

Теоретический материал Задания:

8.

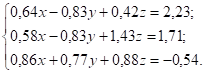
Программа (по Гауссу):

#include.

#include.

#include.

using namespace std;

void sysout (double **a, double *y, int n) {.

for (int i = 0; i < n; i++) {.

for (int j = 0; j < n; j++){.

cout << a[i][j] << «*x» << j;

if (j < n — 1) {.

cout << «+ «;

}.

}.

cout << «= «<< y[i] << endl;

}.

return;

}.

double * gauss (double **a, double *y, int n) {.

double *x, max;

int k, index;

const double eps = 0.1;

x = new double[n];

k = 0;

while (k < n) {.

// Поиск строки с максимальным a[i][k].

max = abs (a[k][k]);

index = k;

for (int i = k + 1; i < n; i++) {.

if (abs (a[i][k]) > max) {.

max = abs (a[i][k]);

index = i;

}.

}.

// Перестановка строк.

if (max < eps) {.

// нет ненулевых диагональных элементов.

cout << «Решение получить невозможно из-за нулевого столбца » ;

cout << index << «матрицы A» << endl;

return 0;

}.

for (int j = 0; j < n; j++) {.

double temp = a[k][j];

a[k][j] = a[index][j];

a[index][j] = temp;

}.

double temp = y[k];

y[k] = y[index];

y[index] = temp;

// Нормализация уравнений.

for (int i = k; i < n; i++) {.

double temp = a[i][k];

if (abs (temp) < eps) continue;

for (int j = 0; j < n; j++) {.

a[i][j] = a[i][j] / temp;

}.

y[i] = y[i] / temp;

if (i == k) continue;

for (int j = 0; j < n; j++) {.

a[i][j] = a[i][j] - a[k][j];

}.

y[i] = y[i] - y[k];

}.

k++;

}.

for (k = n — 1; k >= 0; k—) {.

x[k] = y[k];

for (int i = 0; i < k; i++) {.

y[i] = y[i] - a[i][k] * x[k];

}.

}.

return x;

}.

int main () {.

double **a, *y, *x;

int n;

system («chcp 1251»);

system («cls»);

cout << «Введите количество уравнений: «;

cin >> n;

a = new double*[n];

y = new double[n];

for (int i = 0; i < n; i++) {.

a[i] = new double[n];

for (int j = 0; j < n; j++) {.

cout << «a[» << i << «][» << j << «]= «;

cin >> a[i][j];

}.

}.

for (int i = 0; i < n; i++) {.

cout << «y[» << i << «]= «;

cin >> y[i];

}.

sysout (a, y, n);

x = gauss (a, y, n);

for (int i = 0; i < n; i++){.

cout << «x[» << i << «]=» << x[i] << endl;

}.

cin.get (); cin. get ();

return 0;

}.

Результат: x1=0.86; x2=0.86; x3=-0.137; x4=-0.221.

Программа (по Крамера):

#include.

#include.

using namespace std;

long long det (int x[3][3]).

{.

return 0.64*0.83*0.88+.

• 0.58 *0.77*0.42+
• 0.83 *1.43*0.86-
• 0.86 *0.83*0.42-
• 0.77 *1.43*0.64-
• 0.83 *0.58*0.88;

}.

long long dek (int x[3][3]).

{.

return 2,23*0.83*0.88+.

• 1,71*0.77*0.42+
• 0.83 *1.43*0,54-
• 0,54*0.83*0.42-
• 0.77 *1.43*2,23-
• 0.83 *1,71*0.88;

}.

long long dep (int x[3][3]).

{.

return 0.64*1.71*0.88+.

• 0.58 *0.54*0.42+
• 2.23 *1.43*0.86-
• 0.86 *1.71*0.42-
• 0.54 *1.43*0.64-
• 2.23 *0.58*0.88;

}.

long long dem (int x[3][3]).

{.

return 0.64*0.83*0.54+.

• 0.58 *0.77*2.23+
• 0.83 *1.71*0.86-
• 0.86 *0.83*2.23-
• 0.77 *1.43*0.64-
• 0.83 *0.58*0.88;

}.

int main ().

{.

int a[3][3], n=3;

if (det (a)==0).

cout << «Sistema imeet beskonechnoe kol-vo reshenii ili nesovmestna» ;

else.

cout << «Opredelitel' matrici: «<< det (a) << endl;

cout << «Opredelitel 1: «<< dek (a)/det (a);

cout << «Opredelitel 2: «<< dep (a)/det (a);

cout << «Opredelitel 3: «<< dem (a)/det (a);

system («pause»);

return 0;}.

Результат: x1=-33.5; x2=-29.8; x3=2.5.